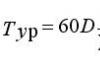Sa artikulong ito, susuriin natin ang konsepto ng cross product ng dalawang vectors. Ibibigay namin ang mga kinakailangang kahulugan, magsulat ng isang formula para sa paghahanap ng mga coordinate ng isang produkto ng vector, ilista at bigyang-katwiran ang mga katangian nito. Pagkatapos nito, tatalakayin natin ang geometric na kahulugan ng produkto ng vector ng dalawang vectors at isaalang-alang ang mga solusyon sa iba't ibang tipikal na halimbawa.

Pag-navigate sa pahina.

Kahulugan ng cross product.

Bago tukuyin ang isang produkto ng vector, unawain natin ang oryentasyon ng isang nakaayos na triple ng mga vector sa tatlong-dimensional na espasyo.

I-plot natin ang mga vectors mula sa isang punto. Depende sa direksyon ng vector, ang tatlo ay maaaring kanan o kaliwa. Tingnan natin mula sa dulo ng vector kung paano ang pinakamaikling pagliko mula sa vector patungo sa . Kung ang pinakamaikling pag-ikot ay nangyayari sa counterclockwise, kung gayon ang triple ng mga vector ay tinatawag tama, kung hindi - umalis.

Ngayon ay kumuha tayo ng dalawang di-collinear na vector at . I-plot natin ang mga vector at mula sa punto A. Bumuo tayo ng ilang vector na patayo sa pareho at at . Malinaw, kapag gumagawa ng isang vector, maaari tayong gumawa ng dalawang bagay, na nagbibigay ito ng alinman sa isang direksyon o ang kabaligtaran (tingnan ang ilustrasyon).

Depende sa direksyon ng vector, ang iniutos na triplet ng mga vector ay maaaring right-handed o left-handed.

Ito ay naglalapit sa atin sa kahulugan ng isang produkto ng vector. Ito ay ibinigay para sa dalawang vectors na tinukoy sa isang hugis-parihaba na coordinate system ng tatlong-dimensional na espasyo.

Kahulugan.

Ang cross product ng dalawang vectors at , na tinukoy sa isang rectangular coordinate system ng tatlong-dimensional na espasyo, ay tinatawag na vector na

Ang cross product ng mga vectors at tinutukoy bilang .

Mga coordinate ng produkto ng vector.

Ngayon ay ibibigay namin ang pangalawang kahulugan ng isang produkto ng vector, na nagbibigay-daan sa iyo upang mahanap ang mga coordinate nito mula sa mga coordinate ng ibinigay na mga vector at.

Kahulugan.

Sa isang rectangular coordinate system ng three-dimensional na espasyo produkto ng vector ng dalawang vector At ay isang vector , nasaan ang mga coordinate vectors.

Ang kahulugang ito ay nagbibigay sa amin ng cross product sa coordinate form.

Ito ay maginhawa upang kumatawan sa produkto ng vector bilang ang determinant ng isang third-order square matrix, ang unang hilera kung saan ay ang mga vectors, ang pangalawang hilera ay naglalaman ng mga coordinate ng vector, at ang pangatlo ay naglalaman ng mga coordinate ng vector sa isang naibigay na rectangular coordinate system:

Kung palawakin natin ang determinant na ito sa mga elemento ng unang hilera, makukuha natin ang pagkakapantay-pantay mula sa kahulugan ng produkto ng vector sa mga coordinate (kung kinakailangan, sumangguni sa artikulo):

Dapat tandaan na ang coordinate form ng produkto ng vector ay ganap na naaayon sa kahulugan na ibinigay sa unang talata ng artikulong ito. Bukod dito, ang dalawang kahulugang ito ng isang cross product ay katumbas. Makikita mo ang patunay ng katotohanang ito sa aklat na nakalista sa dulo ng artikulo.

Mga katangian ng isang produkto ng vector.

Dahil ang produkto ng vector sa mga coordinate ay maaaring katawanin bilang isang determinant ng matrix, ang mga sumusunod ay madaling mabigyang-katwiran batay sa mga katangian ng cross product:

Bilang halimbawa, patunayan natin ang anticommutative property ng isang vector product.

A-prioryo At . Alam namin na ang halaga ng determinant ng isang matrix ay nababaligtad kung ang dalawang hanay ay ipinagpalit, samakatuwid, , na nagpapatunay sa anticommutative na katangian ng isang produkto ng vector.

Vector product - mga halimbawa at solusyon.

Mayroong pangunahing tatlong uri ng mga problema.

Sa mga problema ng unang uri, ang mga haba ng dalawang vector at ang anggulo sa pagitan ng mga ito ay ibinibigay, at kailangan mong hanapin ang haba ng produkto ng vector. Sa kasong ito, ginagamit ang formula .

Halimbawa.

Hanapin ang haba ng produkto ng vector ng mga vector at , kung kilala .

Solusyon.

Alam namin mula sa kahulugan na ang haba ng produkto ng vector ng mga vector at ay katumbas ng produkto ng mga haba ng mga vector at sa pamamagitan ng sine ng anggulo sa pagitan nila, samakatuwid, .

Sagot:

.

Ang mga problema ng pangalawang uri ay nauugnay sa mga coordinate ng mga vector, kung saan ang produkto ng vector, ang haba nito o anupaman ay hinahanap sa pamamagitan ng mga coordinate ng mga ibinigay na vector. At .

Mayroong maraming iba't ibang mga pagpipilian na posible dito. Halimbawa, hindi ang mga coordinate ng mga vector at maaaring tukuyin, ngunit ang kanilang mga pagpapalawak sa mga coordinate na vector ng form at , o mga vector at maaaring tukuyin sa pamamagitan ng mga coordinate ng kanilang mga punto ng pagsisimula at pagtatapos.

Tingnan natin ang mga karaniwang halimbawa.

Halimbawa.

Dalawang vector ang ibinibigay sa isang rectangular coordinate system . Hanapin ang kanilang cross product.

Solusyon.

Ayon sa pangalawang kahulugan, ang produkto ng vector ng dalawang mga vector sa mga coordinate ay nakasulat bilang:

Narating namin ang parehong resulta kung ang produkto ng vector ay isinulat sa mga tuntunin ng determinant

Sagot:

.

Halimbawa.

Hanapin ang haba ng vector product ng mga vectors at , kung saan ang mga unit vectors ng rectangular Cartesian coordinate system.

Solusyon.

Una naming mahanap ang mga coordinate ng produkto ng vector sa isang ibinigay na rectangular coordinate system.

Dahil ang mga vector at may mga coordinate at ayon sa pagkakabanggit (kung kinakailangan, tingnan ang artikulong mga coordinate ng isang vector sa isang rectangular coordinate system), pagkatapos ay sa pamamagitan ng pangalawang kahulugan ng isang produkto ng vector mayroon kami

Iyon ay, ang produkto ng vector ay may mga coordinate sa isang ibinigay na coordinate system.

Nahanap namin ang haba ng isang produkto ng vector bilang square root ng kabuuan ng mga parisukat ng mga coordinate nito (nakuha namin ang formula na ito para sa haba ng isang vector sa seksyon sa paghahanap ng haba ng isang vector):

Sagot:

.

Halimbawa.

Sa isang hugis-parihaba na Cartesian coordinate system, ang mga coordinate ng tatlong puntos ay ibinibigay. Maghanap ng ilang vector na patayo at sa parehong oras.

Solusyon.

Mga Vector at may mga coordinate at ayon sa pagkakabanggit (tingnan ang artikulo sa paghahanap ng mga coordinate ng isang vector sa pamamagitan ng mga coordinate ng mga puntos). Kung makikita natin ang produkto ng vector ng mga vector at , kung gayon sa kahulugan ito ay isang vector na patayo sa parehong to at to , iyon ay, ito ay isang solusyon sa ating problema. Hanapin natin siya

Sagot:

- isa sa mga patayong vector.

Sa mga problema ng ikatlong uri, ang kasanayan sa paggamit ng mga katangian ng produkto ng vector ng mga vector ay nasubok. Pagkatapos ilapat ang mga katangian, inilapat ang kaukulang mga formula.

Halimbawa.

Ang mga vector at ay patayo at ang kanilang mga haba ay 3 at 4, ayon sa pagkakabanggit. Hanapin ang haba ng cross product .

Solusyon.

Sa pamamagitan ng distributive property ng isang vector product, maaari tayong sumulat

Dahil sa kumbinasyonal na pag-aari, inaalis namin ang mga numerical coefficient mula sa tanda ng mga produkto ng vector sa huling expression:

Ang mga produkto ng vector at ay katumbas ng zero, dahil At , Pagkatapos.

Dahil ang produkto ng vector ay anticommutative, kung gayon .

Kaya, gamit ang mga katangian ng produkto ng vector, nakarating kami sa pagkakapantay-pantay .

Sa pamamagitan ng kundisyon, ang mga vector at ay patayo, iyon ay, ang anggulo sa pagitan ng mga ito ay katumbas ng . Iyon ay, mayroon kaming lahat ng data upang mahanap ang kinakailangang haba

Sagot:

.

Geometric na kahulugan ng isang produkto ng vector.

Sa pamamagitan ng kahulugan, ang haba ng produkto ng vector ng mga vectors ay . At mula sa kursong geometry sa mataas na paaralan alam natin na ang lugar ng isang tatsulok ay katumbas ng kalahati ng produkto ng mga haba ng dalawang gilid ng tatsulok at ang sine ng anggulo sa pagitan nila. Dahil dito, ang haba ng produkto ng vector ay katumbas ng dalawang beses sa lugar ng isang tatsulok na ang mga gilid ay ang mga vector at , kung sila ay naka-plot mula sa isang punto. Sa madaling salita, ang haba ng produkto ng vector ng mga vector at katumbas ng lugar ng isang paralelogram na may mga gilid at at ang anggulo sa pagitan ng mga ito ay katumbas ng . Ito ang geometric na kahulugan ng produkto ng vector.

HALONG PRODUKTO NG TATLONG VECTOR AT MGA KATANGIAN NITO

Pinaghalong trabaho tatlong vector ay tinatawag na isang numero na katumbas ng . Itinalaga . Dito, ang unang dalawang vector ay pinarami ng vector at pagkatapos ay ang resultang vector ay pinarami ng scalarly ng ikatlong vector. Malinaw, ang naturang produkto ay isang tiyak na numero.

Isaalang-alang natin ang mga katangian ng isang halo-halong produkto.

1. Geometric na kahulugan pinaghalong gawain. Ang pinaghalong produkto ng 3 vectors, hanggang sa isang sign, ay katumbas ng dami ng parallelepiped na binuo sa mga vector na ito, tulad ng sa mga gilid, i.e. .

   Kaya, at .

   

   Patunay. Isantabi natin ang mga vectors mula sa karaniwang pinagmulan at bumuo ng parallelepiped sa kanila. Ipahiwatig at tandaan natin na . Sa pamamagitan ng kahulugan ng scalar product

   Ipagpalagay na at denoting sa pamamagitan ng h hanapin ang taas ng parallelepiped.

   Kaya, kapag

   Kung, kung gayon. Kaya naman, .

   Ang pagsasama-sama ng parehong mga kasong ito, makakakuha tayo ng o .

   Mula sa patunay ng ari-arian na ito, sa partikular, sumusunod na kung ang triple ng mga vector ay kanang kamay, kung gayon ang pinaghalong produkto ay , at kung ito ay kaliwete, kung gayon .

2. Para sa anumang mga vectors , , ang pagkakapantay-pantay ay totoo

   Ang patunay ng property na ito ay sumusunod mula sa Property 1. Sa katunayan, madaling ipakita iyon at . Bukod dito, ang mga palatandaan na "+" at "-" ay kinuha nang sabay-sabay, dahil ang mga anggulo sa pagitan ng mga vector at at at ay parehong talamak at mahina.

3. Kapag ang alinmang dalawang salik ay muling inayos, nagbabago ang tanda ng pinaghalong produkto.

   Sa katunayan, kung isasaalang-alang natin ang isang halo-halong produkto, kung gayon, halimbawa, o

4. Isang halo-halong produkto kung at kung ang isa sa mga kadahilanan ay katumbas ng zero o ang mga vector ay coplanar.

   Patunay.

   Kaya, ang isang kinakailangan at sapat na kondisyon para sa coplanarity ng 3 vectors ay ang kanilang pinaghalong produkto ay katumbas ng zero. Bilang karagdagan, sumusunod na ang tatlong vector ay bumubuo ng batayan sa espasyo kung .

   Kung ang mga vector ay ibinibigay sa coordinate form, maaari itong ipakita na ang kanilang pinaghalong produkto ay matatagpuan sa pamamagitan ng formula:

   .

   Kaya, ang pinaghalong produkto ay katumbas ng third-order determinant, na mayroong mga coordinate ng unang vector sa unang linya, ang mga coordinate ng pangalawang vector sa pangalawang linya, at ang mga coordinate ng ikatlong vector sa ikatlong linya.

   Mga halimbawa.

ANALYTICAL GEOMETRY SA SPACE

Ang equation F(x, y, z)= 0 ay tumutukoy sa espasyo Oxyz ilang ibabaw, i.e. locus ng mga puntos na ang mga coordinate x, y, z matugunan ang equation na ito. Ang equation na ito ay tinatawag na surface equation, at x, y, z- kasalukuyang mga coordinate.

Gayunpaman, kadalasan ang ibabaw ay hindi tinukoy ng isang equation, ngunit bilang isang hanay ng mga punto sa espasyo na may isa o ibang pag-aari. Sa kasong ito, kinakailangan upang mahanap ang equation ng ibabaw batay sa mga geometric na katangian nito.

EROPLO.

NORMAL NA EROPLO NA VECTOR.

EQUATION NG ISANG EROPLO NA DUMAAN SA ISANG BIGAY NA PUNTO

Isaalang-alang natin ang isang arbitrary na eroplano σ sa kalawakan. Natutukoy ang posisyon nito sa pamamagitan ng pagtukoy ng isang vector na patayo sa eroplanong ito at ilang nakapirming punto M0(x 0, y 0, z 0), nakahiga sa σ plane.

Ang vector na patayo sa eroplanong σ ay tinatawag normal vector ng eroplanong ito. Hayaang may mga coordinate ang vector.

Kunin natin ang equation ng plane σ na dumadaan sa puntong ito M0 at pagkakaroon ng isang normal na vector. Upang gawin ito, kumuha ng di-makatwirang punto sa eroplano σ M(x, y, z) at isaalang-alang ang vector.

Para sa anumang punto M Ang О σ ay isang vector. Samakatuwid, ang kanilang scalar product ay katumbas ng zero. Ang pagkakapantay-pantay na ito ay ang kondisyon na ang punto MО σ. Ito ay may bisa para sa lahat ng mga punto ng eroplanong ito at nilabag kaagad sa punto M ay nasa labas ng σ plane.

Kung tinutukoy natin ang mga puntos sa pamamagitan ng radius vector M, – radius vector ng punto M0, kung gayon ang equation ay maaaring isulat sa anyo

Ang equation na ito ay tinatawag vector equation ng eroplano. Isulat natin ito sa coordinate form. Simula noon

Kaya, nakuha namin ang equation ng eroplano na dumadaan sa puntong ito. Kaya, upang lumikha ng isang equation ng isang eroplano, kailangan mong malaman ang mga coordinate ng normal na vector at ang mga coordinate ng ilang mga punto na nakahiga sa eroplano.

Tandaan na ang equation ng eroplano ay isang equation ng 1st degree na may paggalang sa kasalukuyang mga coordinate x, y At z.

Mga halimbawa.

GENERAL EQUATION NG EROPLO

Maaari itong ipakita na ang anumang first degree equation na may paggalang sa mga coordinate ng Cartesian x, y, z kumakatawan sa equation ng isang tiyak na eroplano. Ang equation na ito ay nakasulat bilang:

Ax+By+Cz+D=0

at tinatawag pangkalahatang equation eroplano, at ang mga coordinate A, B, C narito ang mga coordinate ng normal na vector ng eroplano.

Isaalang-alang natin ang mga espesyal na kaso ng pangkalahatang equation. Alamin natin kung paano matatagpuan ang eroplano na may kaugnayan sa coordinate system kung ang isa o higit pang coefficient ng equation ay naging zero.

Ang A ay ang haba ng segment na pinutol ng eroplano sa axis baka. Katulad nito, maaari itong ipakita na b At c– haba ng mga segment na pinutol ng eroplanong isinasaalang-alang sa mga palakol Oy At Oz.

Maginhawang gamitin ang equation ng isang eroplano sa mga segment upang makagawa ng mga eroplano.

Sa araling ito titingnan natin ang dalawa pang operasyon na may mga vector: produkto ng vector ng mga vector At pinaghalong produkto ng mga vector (Immediate link para sa mga nangangailangan nito). Okay lang, minsan nangyayari na para sa kumpletong kaligayahan, bilang karagdagan sa scalar na produkto ng mga vector, parami nang parami ang kinakailangan. Ito ay pagkagumon sa vector. Maaaring tila tayo ay papasok sa gubat ng analytical geometry. Mali ito. Sa seksyong ito ng mas mataas na matematika, sa pangkalahatan ay may maliit na kahoy, maliban marahil ay sapat para sa Pinocchio. Sa katunayan, ang materyal ay napaka-pangkaraniwan at simple - halos hindi mas kumplikado kaysa sa pareho produktong scalar, magkakaroon ng mas kaunting mga karaniwang gawain. Ang pangunahing bagay sa analytical geometry, dahil marami ang makumbinsi o nakumbinsi na, ay HUWAG MAGKAKAMALI SA PAGKUKULANG. Ulitin tulad ng isang spell at ikaw ay magiging masaya =)

Kung kumikinang ang mga vector sa isang lugar sa malayo, tulad ng kidlat sa abot-tanaw, hindi mahalaga, magsimula sa aralin Mga vector para sa mga dummies upang ibalik o muling makuha ang pangunahing kaalaman tungkol sa mga vector. Ang mas handa na mga mambabasa ay maaaring maging pamilyar sa impormasyon nang pili; sinubukan kong kolektahin ang pinaka kumpletong koleksyon ng mga halimbawa na madalas na matatagpuan sa praktikal na gawain

Ano ang magpapasaya sa iyo kaagad? Noong bata pa ako, nakaka-juggle ako ng dalawa at kahit tatlong bola. Ito ay gumana nang maayos. Ngayon hindi mo na kailangang mag-juggle, dahil isasaalang-alang namin mga spatial vectors lamang, at ang mga flat vector na may dalawang coordinate ay maiiwan. Bakit? Ito ay kung paano ipinanganak ang mga pagkilos na ito - ang vector at pinaghalong produkto ng mga vector ay tinukoy at gumagana sa tatlong-dimensional na espasyo. Mas madali na!

Ang operasyong ito, tulad ng scalar product, ay kinabibilangan dalawang vector. Hayaan itong mga hindi nasisira na mga titik.

Ang aksyon mismo ipinapahiwatig ng sa sumusunod na paraan: . Mayroong iba pang mga pagpipilian, ngunit sanay akong tukuyin ang produkto ng vector ng mga vector sa ganitong paraan, sa mga square bracket na may krus.

At kaagad tanong: kung nasa scalar na produkto ng mga vector dalawang vector ang kasangkot, at dito ang dalawang vector ay pinarami din, pagkatapos ano ang pinagkaiba? Ang malinaw na pagkakaiba ay, una sa lahat, sa RESULTA:

Ang resulta ng scalar product ng mga vectors ay NUMBER:

Ang resulta ng cross product ng mga vectors ay VECTOR: , ibig sabihin, pinaparami natin ang mga vector at muling nakakuha ng isang vector. Saradong club. Actually, dito nagmula ang pangalan ng operasyon. Sa iba't ibang literatura na pang-edukasyon, maaaring mag-iba din ang mga pagtatalaga; Gagamitin ko ang liham.

Kahulugan ng cross product

Una ay magkakaroon ng kahulugan na may larawan, pagkatapos ay magkomento.

Kahulugan: Vector na produkto hindi collinear mga vector, kinuha sa ganitong pagkakasunud-sunod, tinatawag na VECTOR, haba na ayon sa bilang katumbas ng lugar ng paralelogram, na binuo sa mga vector na ito; vector orthogonal sa mga vector, at itinuro upang ang batayan ay may tamang oryentasyon:

Hatiin natin ang kahulugan nang paisa-isa, maraming kawili-wiling bagay dito!

Kaya, ang mga sumusunod na mahahalagang punto ay maaaring i-highlight:

1) Ang orihinal na mga vector, na ipinahiwatig ng mga pulang arrow, ayon sa kahulugan hindi collinear. Angkop na isaalang-alang ang kaso ng mga collinear vectors sa ibang pagkakataon.

2) Kinuha ang mga vector sa isang mahigpit na tinukoy na pagkakasunud-sunod: – Ang "a" ay pinarami ng "maging", hindi "maging" na may "a". Ang resulta ng pagpaparami ng vector ay VECTOR, na nakasaad sa asul. Kung ang mga vector ay pinarami sa reverse order, makakakuha tayo ng isang vector na katumbas ng haba at kabaligtaran sa direksyon (kulay ng raspberry). Ibig sabihin, totoo ang pagkakapantay-pantay .

3) Ngayon, kilalanin natin ang geometric na kahulugan ng produkto ng vector. Ito ay isang napakahalagang punto! Ang LENGTH ng asul na vector (at, samakatuwid, ang crimson vector) ay ayon sa bilang na katumbas ng AREA ng parallelogram na binuo sa mga vector. Sa figure, ang paralelogram na ito ay may kulay na itim.

Tandaan : ang pagguhit ay eskematiko, at, natural, ang nominal na haba ng produkto ng vector ay hindi katumbas ng lugar ng paralelogram.

Alalahanin natin ang isa sa mga geometric na formula: Ang lugar ng isang parallelogram ay katumbas ng produkto ng mga katabing panig at ang sine ng anggulo sa pagitan nila. Samakatuwid, batay sa itaas, ang formula para sa pagkalkula ng LENGTH ng isang produkto ng vector ay wasto:

Binibigyang-diin ko na ang formula ay tungkol sa LENGTH ng vector, at hindi tungkol sa vector mismo. Ano ang praktikal na kahulugan? At ang kahulugan ay sa mga problema ng analytical geometry, ang lugar ng isang paralelogram ay madalas na matatagpuan sa pamamagitan ng konsepto ng isang produkto ng vector:

Kunin natin ang pangalawang mahalagang pormula. Ang dayagonal ng isang paralelogram (pulang may tuldok na linya) ay hinahati ito sa dalawang pantay na tatsulok. Samakatuwid, ang lugar ng isang tatsulok na binuo sa mga vectors (red shading) ay matatagpuan gamit ang formula:

4) Ang isang pantay na mahalagang katotohanan ay ang vector ay orthogonal sa mga vector, iyon ay . Siyempre, ang oppositely directed vector (raspberry arrow) ay orthogonal din sa orihinal na vectors.

5) Ang vector ay nakadirekta sa gayon batayan Mayroon itong tama oryentasyon. Sa aralin tungkol sa paglipat sa isang bagong batayan Nagsalita ako ng sapat na detalye tungkol sa oryentasyon ng eroplano, at ngayon ay malalaman natin kung ano ang oryentasyon sa espasyo. Ipapaliwanag ko sa iyong mga daliri kanang kamay. Mentally combine hintuturo may vector at hinlalato may vector. Ring finger at kalingkingan pindutin ito sa iyong palad. Ang resulta hinlalaki– titingnan ang produkto ng vector. Ito ay isang right-oriented na batayan (ito ang isa sa figure). Ngayon baguhin ang mga vectors ( hintuturo at gitnang daliri) sa ilang mga lugar, bilang isang resulta ang hinlalaki ay iikot, at ang produkto ng vector ay titingin na sa ibaba. Ito rin ay isang batayan na nakatuon sa tama. Maaaring may tanong ka: aling batayan ang umalis sa oryentasyon? "Italaga" sa parehong mga daliri kaliwang kamay vectors, at kunin ang kaliwang batayan at kaliwang oryentasyon ng espasyo (sa kasong ito, ang hinlalaki ay matatagpuan sa direksyon ng mas mababang vector). Sa matalinghagang pagsasalita, ang mga base na ito ay "twist" o i-orient ang espasyo sa iba't ibang direksyon. At ang konsepto na ito ay hindi dapat ituring na isang bagay na malayo o abstract - halimbawa, ang oryentasyon ng espasyo ay binago ng pinaka-ordinaryong salamin, at kung "hinutin mo ang sinasalamin na bagay mula sa salamin," kung gayon sa pangkalahatang kaso ito hindi posibleng pagsamahin ito sa "orihinal." Siyanga pala, hawakan ang tatlong daliri sa salamin at pag-aralan ang reflection ;-)

...gaano kabuti na alam mo na ngayon kanan- at kaliwa-oriented bases, nakakatakot kasi ang mga pahayag ng ilang lecturer tungkol sa pagbabago ng oryentasyon =)

Cross product ng collinear vectors

Ang kahulugan ay tinalakay nang detalyado, nananatili itong malaman kung ano ang mangyayari kapag ang mga vector ay collinear. Kung ang mga vector ay collinear, maaari silang ilagay sa isang tuwid na linya at ang aming parallelogram ay "tupi" din sa isang tuwid na linya. Ang lugar ng ganoon, gaya ng sinasabi ng mga mathematician, mabulok parallelogram ay katumbas ng zero. Ang parehong sumusunod mula sa formula - ang sine ng zero o 180 degrees ay katumbas ng zero, na nangangahulugang ang lugar ay zero

Kaya, kung , pagkatapos At . Mangyaring tandaan na ang produkto ng vector mismo ay katumbas ng zero vector, ngunit sa pagsasanay ito ay madalas na napapabayaan at sila ay nakasulat na ito ay katumbas din ng zero.

Ang isang espesyal na kaso ay ang cross product ng isang vector sa sarili nito:

Gamit ang produkto ng vector, maaari mong suriin ang collinearity ng mga three-dimensional na vector, at susuriin din namin ang problemang ito, bukod sa iba pa.

Upang malutas ang mga praktikal na halimbawa na maaaring kailanganin mo trigonometriko talahanayan upang mahanap ang mga halaga ng mga sine mula dito.

Buweno, pagsikapan natin ang apoy:

Halimbawa 1

a) Hanapin ang haba ng vector product ng mga vectors kung

b) Hanapin ang lugar ng isang paralelogram na binuo sa mga vectors kung

Solusyon: Hindi, hindi ito isang typo, sadyang ginawa kong pareho ang paunang data sa mga sugnay. Dahil mag-iiba ang disenyo ng mga solusyon!

a) Ayon sa kondisyon, kailangan mong hanapin haba vector (krus na produkto). Ayon sa kaukulang formula:

Sagot:

Kung tinanong ka tungkol sa haba, pagkatapos ay sa sagot ay ipinapahiwatig namin ang dimensyon - mga yunit.

b) Ayon sa kondisyon, kailangan mong hanapin parisukat paralelogram na binuo sa mga vector. Ang lugar ng parallelogram na ito ay ayon sa bilang na katumbas ng haba ng produkto ng vector:

Sagot:

Mangyaring tandaan na ang sagot ay hindi nagsasalita tungkol sa produkto ng vector; tinanong kami tungkol sa lugar ng figure, nang naaayon, ang dimensyon ay square units.

Palagi kaming tumitingin sa KUNG ANO ang kailangan naming hanapin ayon sa kondisyon, at, batay dito, bumalangkas kami malinaw sagot. Maaaring mukhang literal ito, ngunit maraming literalista sa mga guro, at ang takdang-aralin ay may magandang pagkakataon na maibalik para sa rebisyon. Kahit na ito ay hindi isang partikular na malayong pag-aalinlangan - kung ang sagot ay mali, kung gayon ang isa ay makakakuha ng impresyon na ang tao ay hindi nauunawaan ang mga simpleng bagay at/o hindi naiintindihan ang kakanyahan ng gawain. Ang puntong ito ay dapat palaging panatilihing nasa ilalim ng kontrol kapag nilulutas ang anumang problema sa mas mataas na matematika, at sa iba pang mga paksa.

Saan napunta ang malaking titik na "en"? Sa prinsipyo, maaari itong maging karagdagan na naka-attach sa solusyon, ngunit upang paikliin ang entry, hindi ko ginawa ito. Sana ay naiintindihan ng lahat iyon at isang pagtatalaga para sa parehong bagay.

Isang tanyag na halimbawa para sa isang solusyon sa DIY:

Halimbawa 2

Hanapin ang lugar ng isang tatsulok na binuo sa mga vectors kung

Ang formula para sa paghahanap ng lugar ng isang tatsulok sa pamamagitan ng produkto ng vector ay ibinibigay sa mga komento sa kahulugan. Ang solusyon at sagot ay nasa katapusan ng aralin.

Sa pagsasagawa, ang gawain ay talagang napakakaraniwan; ang mga tatsulok sa pangkalahatan ay maaaring pahirapan ka.

Upang malutas ang iba pang mga problema kakailanganin namin:

Mga katangian ng produkto ng vector ng mga vector

Isinaalang-alang na namin ang ilang mga katangian ng produkto ng vector, gayunpaman, isasama ko ang mga ito sa listahang ito.

Para sa mga arbitrary na vector at isang arbitrary na numero, ang mga sumusunod na katangian ay totoo:

1) Sa iba pang mga mapagkukunan ng impormasyon, ang item na ito ay karaniwang hindi naka-highlight sa mga katangian, ngunit ito ay napakahalaga sa mga praktikal na termino. Kaya hayaan mo na.

2) – ang ari-arian ay tinalakay din sa itaas, kung minsan ito ay tinatawag anticommutativity. Sa madaling salita, ang pagkakasunud-sunod ng mga vector ay mahalaga.

3) – nag-uugnay o nag-uugnay mga batas ng produkto ng vector. Ang mga constant ay madaling ilipat sa labas ng produkto ng vector. Talaga, ano ang dapat nilang gawin doon?

4) – pamamahagi o distributive mga batas ng produkto ng vector. Wala ring problema sa pagbubukas ng mga bracket.

Upang ipakita, tingnan natin ang isang maikling halimbawa:

Halimbawa 3

Hanapin kung

Solusyon: Ang kundisyon ay muling nangangailangan ng paghahanap ng haba ng produkto ng vector. Ipinta natin ang ating miniature:

(1) Ayon sa mga nauugnay na batas, kinukuha namin ang mga constant sa labas ng saklaw ng produkto ng vector.

(2) Inililipat namin ang constant sa labas ng module, at ang module ay "kumakain" ng minus sign. Ang haba ay hindi maaaring negatibo.

(3) Ang natitira ay malinaw.

Sagot:

Panahon na upang magdagdag ng higit pang kahoy sa apoy:

Halimbawa 4

Kalkulahin ang lugar ng isang tatsulok na binuo sa mga vectors kung

Solusyon: Hanapin ang lugar ng tatsulok gamit ang formula . Ang catch ay ang mga vector na "tse" at "de" ay ipinakita mismo bilang mga kabuuan ng mga vector. Ang algorithm dito ay pamantayan at medyo nakapagpapaalaala sa mga halimbawa No. 3 at 4 ng aralin Tuldok na produkto ng mga vector. Para sa kalinawan, hahatiin namin ang solusyon sa tatlong yugto:

1) Sa unang hakbang, ipinapahayag namin ang produkto ng vector sa pamamagitan ng produkto ng vector, sa katunayan, ipahayag natin ang isang vector sa mga tuntunin ng isang vector. Wala pang salita sa haba!

(1) Palitan ang mga expression ng mga vector.

(2) Gamit ang mga batas sa pamamahagi, binubuksan namin ang mga bracket ayon sa panuntunan ng pagpaparami ng mga polynomial.

(3) Gamit ang mga nauugnay na batas, inililipat namin ang lahat ng mga constant sa kabila ng mga produkto ng vector. Sa kaunting karanasan, ang mga hakbang 2 at 3 ay maaaring isagawa nang sabay-sabay.

(4) Ang una at huling termino ay katumbas ng zero (zero vector) dahil sa magandang katangian. Sa pangalawang termino ginagamit namin ang pag-aari ng anticommutativity ng isang produkto ng vector:

(5) Nagpapakita kami ng mga katulad na termino.

Bilang isang resulta, ang vector ay lumabas na ipinahayag sa pamamagitan ng isang vector, na kung ano ang kinakailangan upang makamit:

2) Sa pangalawang hakbang, nakita namin ang haba ng produkto ng vector na kailangan namin. Ang pagkilos na ito ay katulad ng Halimbawa 3:

3) Hanapin ang lugar ng kinakailangang tatsulok:

Ang mga yugto 2-3 ng solusyon ay maaaring nakasulat sa isang linya.

Sagot:

Ang problemang isinasaalang-alang ay karaniwan sa mga pagsusulit, narito ang isang halimbawa para sa paglutas nito sa iyong sarili:

Halimbawa 5

Hanapin kung

Isang maikling solusyon at sagot sa pagtatapos ng aralin. Tingnan natin kung gaano ka naging matulungin sa pag-aaral ng mga nakaraang halimbawa ;-)

Cross product ng mga vector sa mga coordinate

, na tinukoy sa isang orthonormal na batayan, ipinahayag ng pormula:

Ang formula ay talagang simple: sa tuktok na linya ng determinant isinulat namin ang mga coordinate vectors, sa pangalawa at pangatlong linya ay "inilalagay" namin ang mga coordinate ng mga vector, at inilalagay namin sa mahigpit na pagkakasunud-sunod– una ang mga coordinate ng "ve" vector, pagkatapos ay ang mga coordinate ng "double-ve" vector. Kung ang mga vector ay kailangang i-multiply sa ibang pagkakasunud-sunod, ang mga hilera ay dapat na palitan:

Halimbawa 10

Suriin kung ang mga sumusunod na space vector ay collinear:
A)
b)

Solusyon: Ang tseke ay batay sa isa sa mga pahayag sa araling ito: kung ang mga vector ay collinear, kung gayon ang kanilang produkto ng vector ay katumbas ng zero (zero vector): .

a) Hanapin ang produkto ng vector:

Kaya, ang mga vector ay hindi collinear.

b) Hanapin ang produkto ng vector:

Sagot: a) hindi collinear, b)

Narito, marahil, ang lahat ng pangunahing impormasyon tungkol sa produkto ng vector ng mga vector.

Ang seksyong ito ay hindi magiging napakalaki, dahil kakaunti ang mga problema kung saan ginagamit ang pinaghalong produkto ng mga vector. Sa katunayan, ang lahat ay depende sa kahulugan, geometric na kahulugan at isang pares ng mga gumaganang formula.

Ang isang halo-halong produkto ng mga vector ay ang produkto ng tatlong mga vector:

Kaya't pumila sila na parang tren at hindi makapaghintay na makilala.

Una, muli, isang kahulugan at isang larawan:

Kahulugan: Pinaghalong trabaho hindi koplanar mga vector, kinuha sa ganitong pagkakasunud-sunod, tinawag parallelepiped na dami, na binuo sa mga vectors na ito, na nilagyan ng "+" sign kung ang batayan ay tama, at isang "–" sign kung ang batayan ay naiwan.

Gawin natin ang pagguhit. Ang mga linyang hindi natin nakikita ay iginuhit ng mga tuldok na linya:

Sumisid tayo sa kahulugan:

2) Kinuha ang mga vector sa isang tiyak na pagkakasunud-sunod, iyon ay, ang muling pagsasaayos ng mga vector sa produkto, tulad ng maaari mong hulaan, ay hindi mangyayari nang walang mga kahihinatnan.

3) Bago magkomento sa geometric na kahulugan, mapapansin ko ang isang malinaw na katotohanan: ang pinaghalong produkto ng mga vector ay isang NUMBER: . Sa literatura na pang-edukasyon, ang disenyo ay maaaring bahagyang naiiba; Sanay akong tukuyin ang isang halo-halong produkto ng , at ang resulta ng mga kalkulasyon sa pamamagitan ng titik na "pe".

A-prioryo ang pinaghalong produkto ay ang dami ng parallelepiped, na binuo sa mga vectors (ang figure ay iginuhit na may mga pulang vector at itim na linya). Iyon ay, ang numero ay katumbas ng dami ng isang ibinigay na parallelepiped.

Tandaan : Ang pagguhit ay eskematiko.

4) Huwag na nating alalahanin muli ang konsepto ng oryentasyon ng batayan at espasyo. Ang kahulugan ng huling bahagi ay maaaring magdagdag ng minus sign sa volume. Sa simpleng salita, ang isang halo-halong produkto ay maaaring negatibo: .

Direkta mula sa kahulugan ay sumusunod sa formula para sa pagkalkula ng dami ng isang parallelepiped na binuo sa mga vectors.

Bago ibigay ang konsepto ng isang produkto ng vector, buksan natin ang tanong ng oryentasyon ng isang ordered triple ng mga vectors a →, b →, c → sa tatlong-dimensional na espasyo.

Upang magsimula, isantabi natin ang mga vectors a → , b → , c → mula sa isang punto. Ang oryentasyon ng triple a → , b → , c → ay maaaring kanan o kaliwa, depende sa direksyon ng vector c → mismo. Ang uri ng triple a → , b → , c → ay matutukoy mula sa direksyon kung saan ang pinakamaikling pagliko ay ginawa mula sa vector a → hanggang b → mula sa dulo ng vector c → .

Kung ang pinakamaikling pagliko ay isinasagawa nang pakaliwa, kung gayon ang triple ng mga vectors a → , b → , c → ay tinatawag tama, kung clockwise – umalis.

Susunod, kumuha ng dalawang non-collinear vectors a → at b →. I-plot natin ang mga vectors A B → = a → at A C → = b → mula sa punto A. Bumuo tayo ng isang vector A D → = c →, na sabay na patayo sa parehong A B → at A C →. Kaya, kapag itinatayo ang vector mismo A D → = c →, magagawa natin ang dalawang bagay, na nagbibigay ito ng alinman sa isang direksyon o ang kabaligtaran (tingnan ang ilustrasyon).

Ang nakaayos na triple ng mga vectors a → , b → , c → ay maaaring, tulad ng nalaman namin, pakanan o pakaliwa depende sa direksyon ng vector.

Mula sa itaas maaari nating ipakilala ang kahulugan ng isang produkto ng vector. Ang kahulugan na ito ay ibinigay para sa dalawang vector na tinukoy sa isang hugis-parihaba na coordinate system ng tatlong-dimensional na espasyo.

Kahulugan 1

Ang produkto ng vector ng dalawang vectors a → at b → tatawagin natin ang tulad ng isang vector na tinukoy sa isang hugis-parihaba na coordinate system ng tatlong-dimensional na espasyo tulad na:

• kung ang mga vectors a → at b → ay collinear, ito ay magiging zero;
• ito ay magiging patayo sa parehong vector a → ​​​​ at vector b → i.e. ∠ a → c → = ∠ b → c → = π 2 ;
• ang haba nito ay tinutukoy ng formula: c → = a → · b → · sin ∠ a → , b → ;
• ang triple ng mga vectors a → , b → , c → ay may parehong oryentasyon gaya ng ibinigay na coordinate system.

Ang produkto ng vector ng mga vectors a → at b → ay may sumusunod na notasyon: a → × b →.

Mga coordinate ng produkto ng vector

Dahil ang anumang vector ay may ilang partikular na coordinate sa sistema ng coordinate, maaari tayong magpakilala ng pangalawang kahulugan ng isang produkto ng vector, na magbibigay-daan sa amin upang mahanap ang mga coordinate nito gamit ang ibinigay na mga coordinate ng mga vector.

Kahulugan 2

Sa isang rectangular coordinate system ng three-dimensional na espasyo produkto ng vector ng dalawang vector a → = (a x ; a y ; a z) at b → = (b x ; b y ; b z) ay tinatawag na vector c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , kung saan ang i → , j → , k → ay mga coordinate vector.

Ang produkto ng vector ay maaaring katawanin bilang determinant ng isang third-order square matrix, kung saan ang unang hilera ay naglalaman ng mga vector vectors i → , j → , k → , ang pangalawang hilera ay naglalaman ng mga coordinate ng vector a → , at ang ikatlong hilera naglalaman ng mga coordinate ng vector b → sa isang ibinigay na rectangular coordinate system, ito ang determinant ng matrix na ganito ang hitsura: c → = a → × b → = i → j → k → a x a y a z b x b y b z

Ang pagpapalawak ng determinant na ito sa mga elemento ng unang hilera, nakukuha natin ang pagkakapantay-pantay: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · i → - a x a z b x b z · j → + a x a y b x b = y → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →

Mga katangian ng isang cross product

Ito ay kilala na ang produkto ng vector sa mga coordinate ay kinakatawan bilang ang determinant ng matrix c → = a → × b → = i → j → k → a x a y a z b x b y b z , pagkatapos ay sa batayan katangian ng matrix determinant ang mga sumusunod ay ipinapakita katangian ng isang produkto ng vector:

1. anticommutativity a → × b → = - b → × a → ;
2. distributivity a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → o a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
3. associativity λ a → × b → = λ a → × b → o a → × (λ b →) = λ a → × b →, kung saan ang λ ay isang arbitrary real number.

Ang mga katangiang ito ay may mga simpleng patunay.

Bilang halimbawa, maaari nating patunayan ang anticommutative na katangian ng isang produkto ng vector.

Patunay ng anticommutativity

Sa kahulugan, a → × b → = i → j → k → a x a y a z b x b y b z at b → × a → = i → j → k → b x b y b z a x a y a z . At kung ang dalawang hilera ng matrix ay ipinagpalit, kung gayon ang halaga ng determinant ng matrix ay dapat magbago sa kabaligtaran, samakatuwid, a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → , na at nagpapatunay na ang produkto ng vector ay anticommutative.

Vector product - mga halimbawa at solusyon

Sa karamihan ng mga kaso, mayroong tatlong uri ng mga problema.

Sa mga problema ng unang uri, ang mga haba ng dalawang vector at ang anggulo sa pagitan ng mga ito ay karaniwang ibinibigay, at kailangan mong hanapin ang haba ng produkto ng vector. Sa kasong ito, gamitin ang sumusunod na formula c → = a → · b → · sin ∠ a → , b → .

Halimbawa 1

Hanapin ang haba ng vector product ng mga vectors a → at b → kung alam mo ang a → = 3, b → = 5, ∠ a →, b → = π 4.

Solusyon

Sa pamamagitan ng pagtukoy sa haba ng produkto ng vector ng mga vectors a → at b →, malulutas natin ang problemang ito: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .

Sagot: 15 2 2 .

Ang mga problema ng pangalawang uri ay may koneksyon sa mga coordinate ng mga vector, sa kanila ang produkto ng vector, haba nito, atbp. Hinahanap sa pamamagitan ng mga kilalang coordinate ng mga ibinigay na vectors a → = (a x; a y; a z) At b → = (b x ; b y ; b z) .

Para sa ganitong uri ng problema, maaari mong malutas ang maraming mga pagpipilian sa gawain. Halimbawa, hindi maaaring tukuyin ang mga coordinate ng mga vectors a → at b →, ngunit ang kanilang mga pagpapalawak sa mga coordinate vector ng form b → = b x · i → + b y · j → + b z · k → at c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →, o ang mga vectors a → at b → ay maaaring tukuyin ng mga coordinate ng kanilang simula at mga punto ng pagtatapos.

Isaalang-alang ang sumusunod na mga halimbawa.

Halimbawa 2

Sa isang rectangular coordinate system, dalawang vector ang ibinibigay: a → = (2; 1; - 3), b → = (0; - 1; 1). Hanapin ang kanilang cross product.

Solusyon

Sa pangalawang kahulugan, makikita natin ang produkto ng vector ng dalawang vector sa ibinigay na mga coordinate: a → × b → = (a y · b z - a z · b y) · i → + (a z · b x - a x · b z) · j → + ( a x · b y - a y · b x) · k → = = (1 · 1 - (- 3) · (- 1)) · i → + ((- 3) · 0 - 2 · 1) · j → + (2 · (- 1) - 1 · 0) · k → = = - 2 i → - 2 j → - 2 k → .

Kung isusulat natin ang produkto ng vector sa pamamagitan ng determinant ng matrix, magiging ganito ang solusyon sa halimbawang ito: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .

Sagot: a → × b → = - 2 i → - 2 j → - 2 k → .

Halimbawa 3

Hanapin ang haba ng vector product ng mga vectors i → - j → at i → + j → + k →, kung saan ang i →, j →, k → ay ang mga unit vectors ng rectangular Cartesian coordinate system.

Solusyon

Una, hanapin natin ang mga coordinate ng isang ibinigay na produkto ng vector i → - j → × i → + j → + k → sa isang ibinigay na rectangular coordinate system.

Ito ay kilala na ang mga vectors i → - j → at i → + j → + k → ay may mga coordinate (1; - 1; 0) at (1; 1; 1), ayon sa pagkakabanggit. Hanapin natin ang haba ng produkto ng vector gamit ang determinant ng matrix, pagkatapos ay mayroon tayong i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .

Samakatuwid, ang produkto ng vector i → - j → × i → + j → + k → ay may mga coordinate (- 1 ; - 1 ; 2) sa ibinigay na coordinate system.

Hinahanap namin ang haba ng produkto ng vector gamit ang formula (tingnan ang seksyon sa paghahanap ng haba ng isang vector): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6.

Sagot: i → - j → × i → + j → + k → = 6 . .

Halimbawa 4

Sa isang hugis-parihaba na sistema ng coordinate ng Cartesian, ang mga coordinate ng tatlong puntos na A (1, 0, 1), B (0, 2, 3), C (1, 4, 2) ay ibinibigay. Maghanap ng ilang vector na patayo sa A B → at A C → sa parehong oras.

Solusyon

Ang mga Vector A B → at A C → ay may mga sumusunod na coordinate (- 1 ; 2 ; 2) at (0 ; 4 ; 1) ayon sa pagkakabanggit. Ang pagkakaroon ng natagpuan ang produkto ng vector ng mga vectors A B → at A C →, malinaw na ito ay isang patayong vector sa pamamagitan ng kahulugan sa parehong A B → at A C →, iyon ay, ito ay isang solusyon sa ating problema. Hanapin natin A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .

Sagot: - 6 i → + j → - 4 k → . - isa sa mga patayong vector.

Ang mga problema ng ikatlong uri ay nakatuon sa paggamit ng mga katangian ng produkto ng vector ng mga vector. Pagkatapos mag-apply kung alin, makakakuha tayo ng solusyon sa ibinigay na problema.

Halimbawa 5

Ang mga vectors a → at b → ay patayo at ang kanilang mga haba ay 3 at 4, ayon sa pagkakabanggit. Hanapin ang haba ng vector product 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → .

Solusyon

Sa pamamagitan ng distributive property ng isang vector product, maaari nating isulat ang 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →

Sa pamamagitan ng pag-aari ng associativity, kinuha namin ang mga numerical coefficients mula sa tanda ng mga produkto ng vector sa huling expression: 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → = = 3 · a → × a → + 3 · (- 2) · a → × b → + (- 1) · b → × a → + (- 1) · (- 2) · b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →

Ang mga produktong vector a → × a → at b → × b → ay katumbas ng 0, dahil a → × a → = a → · a → · sin 0 = 0 at b → × b → = b → · b → · sin 0 = 0, pagkatapos ay 3 · a → × a → - 6 · a → × b → - b → × a → + 2 · b → × b → = - 6 · a → × b → - b → × a → . .

Mula sa anticommutativity ng vector product ito ay sumusunod - 6 · a → × b → - b → × a → = - 6 · a → × b → - (- 1) · a → × b → = - 5 · a → × b → . .

Gamit ang mga katangian ng produkto ng vector, nakukuha natin ang pagkakapantay-pantay 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .

Sa pamamagitan ng kondisyon, ang mga vectors a → at b → ay patayo, iyon ay, ang anggulo sa pagitan ng mga ito ay katumbas ng π 2. Ngayon ang natitira na lang ay palitan ang mga nahanap na halaga sa naaangkop na mga formula: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → · kasalanan (a → , b →) = 5 · 3 · 4 · sin π 2 = 60 .

Sagot: 3 a → - b → × a → - 2 b → = 60.

Ang haba ng vector product ng mga vectors ayon sa kahulugan ay katumbas ng a → × b → = a → · b → · sin ∠ a → , b → . Dahil alam na (mula sa kurso ng paaralan) na ang lugar ng isang tatsulok ay katumbas ng kalahati ng produkto ng mga haba ng dalawang panig nito na pinarami ng sine ng anggulo sa pagitan ng mga panig na ito. Dahil dito, ang haba ng produkto ng vector ay katumbas ng lugar ng parallelogram - isang dobleng tatsulok, lalo na ang produkto ng mga gilid sa anyo ng mga vectors a → at b →, na inilatag mula sa isang punto, ng sine ng ang anggulo sa pagitan nila sin ∠ a →, b →.

Ito ang geometriko na kahulugan ng isang produkto ng vector.

Pisikal na kahulugan ng produkto ng vector

Sa mekanika, isa sa mga sangay ng pisika, salamat sa produkto ng vector, maaari mong matukoy ang sandali ng isang puwersa na nauugnay sa isang punto sa espasyo.

Kahulugan 3

Sa sandali ng puwersa F → inilapat sa punto B, kaugnay sa punto A, mauunawaan natin ang sumusunod na produkto ng vector A B → × F →.

Kung may napansin kang error sa text, paki-highlight ito at pindutin ang Ctrl+Enter

7.1. Kahulugan ng cross product

Tatlong non-coplanar vectors a, b at c, na kinuha sa ipinahiwatig na pagkakasunud-sunod, ay bumubuo ng right-handed triplet kung, mula sa dulo ng ikatlong vector c, ang pinakamaikling pagliko mula sa unang vector a hanggang sa pangalawang vector b ay makikita sa maging counterclockwise, at isang left-handed triplet kung clockwise (tingnan ang Fig. 16).

Ang vector product ng vector a at vector b ay tinatawag na vector c, na:

1. Patayo sa mga vectors a at b, ibig sabihin, c ^ a at c ^ b ;

2. May haba ayon sa bilang na katumbas ng lugar ng isang paralelogram na itinayo sa mga vectors a atb tulad ng sa mga gilid (tingnan ang Fig. 17), i.e.

3. Ang mga vectors a, b at c ay bumubuo ng right-handed triple.

Ang cross product ay tinutukoy ng isang x b o [a,b]. Ang mga sumusunod na ugnayan sa pagitan ng mga vector ng yunit ay direktang sinusunod ko mula sa kahulugan ng produkto ng vector, j At k(tingnan ang Fig. 18):

i x j = k, j x k = i, k x i = j.
Patunayan natin, halimbawa, iyon ako xj = k.

1) k ^ i, k ^ j ;

2) |k |=1, ngunit | ako x j| = |i | |J | kasalanan(90°)=1;

3) mga vector i, j at k bumuo ng isang kanang triple (tingnan ang Fig. 16).

7.2. Mga katangian ng isang cross product

1. Kapag muling inaayos ang mga salik, ang produkto ng vector ay nagbabago ng tanda, i.e. at xb =(b xa) (tingnan ang Fig. 19).

Ang mga vector a xb at b xa ay collinear, may parehong mga module (ang lugar ng parallelogram ay nananatiling hindi nagbabago), ngunit magkasalungat na direksyon (triples a, b, a xb at a, b, b x a ng kabaligtaran na oryentasyon). Yan ay axb = -(b xa).

2. Ang produkto ng vector ay may pinagsamang katangian na may kinalaman sa scalar factor, ibig sabihin, l ​​(a xb) = (l a) x b = a x (l b).

Hayaan ang l >0. Ang Vector l (a xb) ay patayo sa mga vectors a at b. Vector ( l a) x b ay patayo din sa mga vectors a at b(mga vector a, l ngunit nakahiga sa parehong eroplano). Nangangahulugan ito na ang mga vectors l(a xb) at ( l a) x b collinear. Obvious naman na magkasabay ang direksyon nila. Sila ay may parehong haba:

kaya lang l(a xb)= l isang xb. Ito ay pinatunayan sa katulad na paraan para sa l<0.

3. Dalawang di-zero na vector a at b ay collinear kung at kung ang kanilang produkto ng vector ay katumbas ng zero vector, ibig sabihin, isang ||b<=>at xb =0.

Sa partikular, i *i =j *j =k *k =0 .

4. Ang produkto ng vector ay may katangian ng pamamahagi:

(a+b) xc = isang xc + b xs.

Tatanggapin namin nang walang patunay.

7.3. Pagpapahayag ng cross product sa mga tuntunin ng mga coordinate

Gagamitin namin ang cross product table ng mga vectors i, j at k:

kung ang direksyon ng pinakamaikling landas mula sa unang vector hanggang sa pangalawa ay tumutugma sa direksyon ng arrow, kung gayon ang produkto ay katumbas ng pangatlong vector; kung hindi ito nag-tutugma, ang pangatlong vector ay kinuha gamit ang isang minus sign.

Hayaang ibigay ang dalawang vectors a =a x i +a y j+a z k at b = b x i+b y j+b z k. Hanapin natin ang produkto ng vector ng mga vector na ito sa pamamagitan ng pagpaparami sa kanila bilang mga polynomial (ayon sa mga katangian ng produkto ng vector):

Ang resultang formula ay maaaring maisulat nang mas maikli:

dahil ang kanang bahagi ng pagkakapantay-pantay (7.1) ay tumutugma sa pagpapalawak ng third-order determinant sa mga tuntunin ng mga elemento ng unang hilera. Ang pagkakapantay-pantay (7.2) ay madaling matandaan.

7.4. Ang ilang mga aplikasyon ng cross product

Pagtatatag ng collinearity ng mga vectors

Paghahanap ng lugar ng isang paralelogram at isang tatsulok

Ayon sa kahulugan ng produkto ng vector ng mga vectors A at b |a xb | =|a | * |b |sin g, ibig sabihin, mga pares ng S = |a x b |. At, samakatuwid, D S =1/2|a x b |.

Pagpapasiya ng sandali ng puwersa tungkol sa isang punto

Hayaang maglapat ng puwersa sa punto A F =AB bumitaw TUNGKOL SA- ilang punto sa espasyo (tingnan ang Fig. 20).

Ito ay kilala mula sa pisika na sandali ng puwersa F kaugnay sa punto TUNGKOL SA tinatawag na vector M, na dumadaan sa punto TUNGKOL SA At:

1) patayo sa eroplano na dumadaan sa mga punto O, A, B;

2) ayon sa bilang na katumbas ng produkto ng puwersa bawat braso

3) bumubuo ng tamang triple na may mga vectors na OA at A B.

Samakatuwid, M = OA x F.

Paghahanap ng linear na bilis ng pag-ikot

Bilis v point M ng isang matibay na katawan na umiikot na may angular na bilis w sa paligid ng isang nakapirming axis, ay tinutukoy ng formula ni Euler v =w xr, kung saan ang r =OM, kung saan ang O ay ilang nakapirming punto ng axis (tingnan ang Fig. 21).