O escopo e o intervalo da função. Na matemática elementar, as funções são estudadas apenas no conjunto dos números reais R.Isso significa que o argumento da função só pode assumir os valores reais para os quais a função é definida, ou seja, também só aceita valores reais. Um monte de X todos os valores válidos válidos do argumento x, para o qual a função y= f(x) é definido, chamado escopo da função. Um monte de S todos os valores reais y que a função aceita é chamado intervalo de funções. Agora você pode dar mais definição precisa recursos: regra(lei) de correspondência entre os conjuntos X e Y, pelo qual para cada elemento do conjuntoX pode encontrar um e apenas um elemento do conjunto Y, é chamado de função.

Segue-se desta definição que uma função é considerada dada se:

O escopo da função é definido X ;

O escopo da função é definido S ;

A regra (lei) da correspondência é conhecida, e tal que para cada

Apenas um valor de função pode ser encontrado para um valor de argumento.

Este requisito de exclusividade da função é obrigatório.

função monotônica. Se para quaisquer dois valores do argumento x 1 e x 2 da condição x 2 > x 1 segue f(x 2) > f(x 1), então a função f(x) é chamado aumentando; se para qualquer x 1 e x 2 da condição x 2 > x 1 segue f(x 2) < f(x 1), então a função f(x) é chamado minguante. Uma função que só aumenta ou só diminui é chamada monótono.

Funções limitadas e ilimitadas. A função é chamada limitado se existe um número tão positivo M o que | f(x) | M para todos os valores x. Se não existir tal número, então a função é ilimitado.

EXEMPLOS.

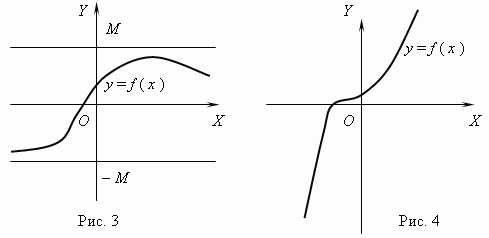
A função representada na Fig. 3 é limitada, mas não monotônica. A função na Figura 4 é exatamente o oposto, monótona, mas ilimitada. (Explique isso por favor!)

Funções contínuas e descontínuas. Função y = f (x) é chamado contínuo no pontox = uma, E se:

1) a função é definida para x = uma, ou seja f (uma) existir;

2) existe finito limite limite f (x) ;

x→uma

(Consulte "Limites de Funções")

3) f (uma) = lim f (x) .

x→uma

Se pelo menos uma dessas condições não for atendida, a função é chamada descontínuo no ponto x = uma.

Se a função é contínua em tudo pontos do seu domínio de definição, então é chamado função contínua.

Funções pares e ímpares. Se para algum x f(- x) = f (x), então a função é chamada até; se for: f(- x) = - f (x), então a função é chamada ímpar. Gráfico de uma função par simétrico em relação ao eixo Y(Fig.5), um gráfico de uma função ímpar Simmétrica sobre a origem(Fig. 6).

Função periódica. Função f (x) - periódico se existe tal diferente de zero número T Pelo que algum x do escopo da definição da função ocorre: f (x + T) = f (x). Tal ao menos o número é chamado período de função. Todas as funções trigonométricas são periódicas.

EXEMPLO 1. Prove que o pecado x tem um período de 2.

SOLUÇÃO Sabemos que o pecado ( x+ 2n) = pecado x, Onde n= 0, ± 1, ± 2, …

Portanto, somando 2 n para o argumento seno

Muda seu valor. Existe outro número com este

Mesma propriedade?

Vamos fingir que P- tal número, ou seja, igualdade:

Pecado ( x+P) = pecado x,

Válido para qualquer valor x. Mas então tem

Localização e x= / 2 , ou seja

pecado(/2 + P) = sen / 2 = 1.

Mas de acordo com a fórmula de redução sin ( / 2 + P) = co P. Então

Segue das duas últimas igualdades que cos P= 1, mas nós

Sabemos que isso só é verdade quando P = 2n. Desde o menor

Um número diferente de zero de 2 né 2, então esse número

E há um período de pecado x. Prova-se igualmente que 2 a partir de né , então este é o período sen 2 x.

Função nula. O valor do argumento para o qual a função é igual a 0 é chamado zero (funções de raiz). Uma função pode ter vários zeros. Por exemplo, a função y = x (x + 1) (x-3) tem três zeros: x= 0, x= -1, x= 3. Geometricamente função nula - é a abcissa do ponto de intersecção do gráfico da função com o eixo X .

A Figura 7 mostra o gráfico da função com zeros: x= uma, x = b e x= c.

Assíntota. Se o gráfico de uma função se aproxima de uma certa linha reta indefinidamente à medida que se afasta da origem, então essa linha reta é chamada assíntota.

Limites e continuidade

Conjuntos

Debaixo muitosé entendido como um conjunto de objetos homogêneos. Os objetos que formam um conjunto são chamados elementos ou pontos este conjunto. Os conjuntos são indicados por letras maiúsculas e seus elementos por letras minúsculas. Se um umaé um elemento do conjunto UMA, então a notação umaÎ UMA. Se um b não é um elemento do conjunto UMA, então fica escrito assim: b Ï UMA. Um conjunto que não contém um único elemento é chamado de conjunto vazio e é denotado da seguinte forma: Ø.

Se o conjunto B consiste em uma parte dos elementos do conjunto UMA ou coincide com ele, então o conjunto B chamado subconjunto define e denota BÌ UMA.

Os dois conjuntos são chamados igual se consistirem dos mesmos elementos.

Associação dois conjuntos UMA e Bé chamado de conjunto C, constituído por todos os elementos pertencentes a pelo menos um dos conjuntos: C=UMAÈ B.

cruzando dois conjuntos UMA e Bé chamado de conjunto C, consistindo de todos os elementos pertencentes a cada um dos conjuntos dados: C=UMAÇ B.

diferença conjuntos UMA e Bé chamado de conjunto E UMA, que não pertencem ao conjunto B: .

Suplemento conjuntos UMAÌ Bé chamado de conjunto C, que consiste em todos os elementos do conjunto B, não pertencente UMA.

Os conjuntos cujos elementos são números reais são chamados numérico:

Em que NÌ ZÌ QÌ R, EUÌ R e R=EUÈ Q.

Um monte de X, cujos elementos satisfazem a desigualdade é chamado segmento(segmento) e denotado por [ uma; b]; desigualdade uma<x<b – intervalo e é denotado por (); desigualdades e - meios-intervalos e são denotados por e , respectivamente. Muitas vezes você também tem que lidar com intervalos infinitos e meios-intervalos: , , , e . É conveniente chamá-los todos nos intervalos .

Intervalo, ou seja o conjunto de pontos que satisfazem a desigualdade (onde ), é chamado -vizinhança do ponto uma.

O conceito de uma função. Principais propriedades da função

Se cada elemento x conjuntos X um único elemento é correspondido y conjuntos S, então dizemos que no conjunto X dado função y=f(x). Em que x chamado variável independente ou argumento, uma y – variável dependente ou função, uma f significa a lei da correspondência. Um monte de X chamado domínio de definição funções, mas o conjunto S – alcance funções.

Existem várias maneiras de definir funções.

1) Método analítico - a função é dada por uma fórmula da forma y=f(x).

2) Método tabular - a função é definida por uma tabela contendo os valores do argumento e os valores da função correspondente y=f(x).

3) Método gráfico - a imagem do gráfico da função, ou seja, conjunto de pontos ( x; y) do plano de coordenadas, cujas abcissas representam os valores do argumento , e as ordenadas são os valores correspondentes da função y=f(x).

4) Método verbal - a função é descrita pela regra de sua compilação. Por exemplo, a função Dirichlet assume o valor 1 se xé um número racional e 0 se xé um número irracional.

As seguintes propriedades principais das funções são distinguidas.

1 Par e ímpar Função y=f(x) é chamado até, se para quaisquer valores x do domínio de sua definição, f(–x)=f(x), e ímpar, E se f(–x)=–f(x). Se nenhuma das equações acima for válida, então y=f(x) é chamado função geral. O gráfico de uma função par é simétrico em relação ao eixo Oi, e o gráfico de uma função ímpar é simétrico em relação à origem.

2 Monotonia Função y=f(x) é chamado aumentando (minguante) no intervalo X, E se maior valor um argumento deste intervalo corresponde a um valor maior (menor) da função. Deixe ser x 1 ,x 2 О X, x 2 >x 1 . Então a função aumenta no intervalo X, E se f(x 2)>f(x 1) e diminui se f(x 2)<f(x 1).

Juntamente com as funções crescentes e decrescentes, são consideradas as funções não decrescentes e não crescentes. A função é chamada não decrescente (não crescente), E se x 1 ,x 2 О X, x 2 >x 1 a desigualdade f(x 2)≥f(x 1) (f(x 2)≤f(x 1)).

Funções crescentes e decrescentes, assim como funções não crescentes e não decrescentes, são chamadas de monótonas.

3 Limitado Função y=f(x) é chamado de limitado no intervalo X se existe um número tão positivo M>0, o que | f(x)|≤M para qualquer um xÎ X. Caso contrário, a função é chamada ilimitada em X.

4 Periodicidade Função y=f(x) é chamado periódico com período T≠0 se para qualquer x fora do escopo da função f(x+T)=f(x). No que segue, o período será entendido como o menor período positivo funções.

A função é chamada explícito, se for dado por uma fórmula da forma y=f(x). Se a função é dada pela equação F(x, y)=0 não permitido em relação à variável dependente y, então é chamado implícito.

Deixe ser y=f(x) é uma função da variável independente definida no conjunto X com alcance S. Vamos combinar cada yÎ S significado único xÎ X, em qual f(x)=y.Então a função resultante x=φ (y) definido no conjunto S com alcance X, é chamado reverter e denotado y=f –1 (x). Gráficos de funções mutuamente inversas são simétricos em relação à bissetriz do primeiro e terceiro quartos das coordenadas.

Deixe a função y=f(você) é uma função da variável você definido no set você com alcance S, e a variável você por sua vez é uma função você=φ (x) definido no conjunto X com alcance você. Então dado no set X função y=f(φ (x)) é chamado função complexa(composição de funções, superposição de funções, função de uma função).

Funções elementares

As principais funções elementares incluem:

• Função liga-desliga y=xn; y=x-n e y=x 1/ n;
• função exponencial y=um x;
• função logarítmica y=log um x;
• funções trigonométricas y= pecado x, y= cos x, y=tg x e y=ctg x;
• funções trigonométricas inversas y= arco seno x, y= arcos x, y=arctg x e y=arctg x.

A partir das funções elementares básicas, novas funções podem ser obtidas usando operações algébricas e superposição de funções.

Funções construídas a partir de funções elementares básicas usando um número finito de operações algébricas e um número finito de operações de superposição são chamadas elementar.

Algébricoé uma função na qual um número finito de operações algébricas é executado no argumento. As funções algébricas incluem:

função racional inteira (polinômio ou polinômio)

função racional fracionária (razão de dois polinômios)

função irracional (se as operações no argumento incluem extração de raiz).

Qualquer função não algébrica é chamada transcendente. As funções transcendentais incluem funções exponenciais, logarítmicas, trigonométricas e trigonométricas inversas.

o material metódicoé apenas para referência e se aplica a uma grande variedade tópicos. O artigo fornece uma visão geral dos gráficos das principais funções elementares e considera a questão mais importante - como construir um gráfico corretamente e RÁPIDO. No curso de matemática superior sem conhecer os gráficos das funções elementares básicas, será difícil, por isso é muito importante lembrar como são os gráficos de uma parábola, hipérbole, seno, cosseno, etc. valores da função. Também falaremos sobre algumas propriedades das funções principais.

Não pretendo a completude e o rigor científico dos materiais, a ênfase será colocada, em primeiro lugar, na prática - aquelas coisas com as quais é preciso enfrentar literalmente a cada passo, em qualquer tópico de matemática superior. Gráficos para manequins? Você pode dizer assim.

Por demanda popular dos leitores índice clicável:

Além disso, há um resumo ultracurto sobre o tema
- domine 16 tipos de gráficos estudando SEIS páginas!

Sério, seis, até eu mesmo fiquei surpreso. Este resumo contém gráficos aprimorados e está disponível por uma taxa nominal, uma versão demo pode ser visualizada. É conveniente imprimir o arquivo para que os gráficos estejam sempre à mão. Obrigado por apoiar o projeto!

E começamos logo:

Como construir eixos coordenados corretamente?

Na prática, as provas são quase sempre elaboradas pelos alunos em cadernos separados, alinhados em uma gaiola. Por que você precisa de marcações quadriculadas? Afinal, o trabalho, em princípio, pode ser feito em folhas A4. E a gaiola é necessária apenas para o design preciso e de alta qualidade dos desenhos.

Qualquer desenho de um gráfico de função começa com eixos de coordenadas.

Os desenhos são bidimensionais e tridimensionais.

Consideremos primeiro o caso bidimensional Sistema de coordenada cartesiana:

1) Nós desenhamos eixos de coordenadas. O eixo é chamado eixo x , e o eixo eixo y . Nós sempre tentamos desenhá-los limpo e não torto. As flechas também não devem se parecer com a barba de Papa Carlo.

2) Assinamos os eixos com letras maiúsculas "x" e "y". Não se esqueça de assinar os eixos.

3) Defina a escala ao longo dos eixos: desenhar zero e dois uns. Ao fazer um desenho, a escala mais conveniente e comum é: 1 unidade = 2 células (desenho à esquerda) - mantenha-a se possível. No entanto, de vez em quando acontece que o desenho não cabe em uma folha de caderno - então reduzimos a escala: 1 unidade = 1 célula (desenho à direita). Raramente, mas acontece que a escala do desenho tem que ser reduzida (ou aumentada) ainda mais

NÃO rabiscar de uma metralhadora ... -5, -4, -3, -1, 0, 1, 2, 3, 4, 5, .... Pois o plano coordenado não é um monumento a Descartes, e o aluno não é uma pomba. Nós colocamos zero e duas unidades ao longo dos eixos. As vezes ao invés de unidades, é conveniente “detectar” outros valores, por exemplo, “dois” no eixo das abcissas e “três” no eixo das ordenadas - e este sistema (0, 2 e 3) também definirá exclusivamente a grade de coordenadas.

É melhor estimar as dimensões estimadas do desenho ANTES do desenho ser desenhado.. Então, por exemplo, se a tarefa requer desenhar um triângulo com vértices , , , então é bastante claro que a escala popular 1 unidade = 2 células não funcionará. Por quê? Vejamos o ponto - aqui você tem que medir quinze centímetros para baixo e, obviamente, o desenho não caberá (ou mal caberá) em uma folha de caderno. Portanto, selecionamos imediatamente uma escala menor 1 unidade = 1 célula.

By the way, cerca de centímetros e células de notebook. É verdade que existem 15 centímetros em 30 células de notebook? Meça em um caderno para juros 15 centímetros com uma régua. Na URSS, talvez isso fosse verdade... É interessante notar que se você medir esses mesmos centímetros na horizontal e na vertical, os resultados (em células) serão diferentes! Estritamente falando, os notebooks modernos não são quadriculados, mas retangulares. Pode parecer bobagem, mas desenhar, por exemplo, um círculo com uma bússola em tais situações é muito inconveniente. Para ser honesto, nesses momentos você começa a pensar na correção do camarada Stalin, que foi enviado para campos de trabalho hacker na produção, sem mencionar a indústria automotiva doméstica, aviões caindo ou usinas elétricas explodindo.

Falando em qualidade, ou uma breve recomendação sobre papelaria. Até hoje, a maioria dos cadernos à venda, sem dizer palavrões, são goblins completos. Pelo motivo de ficarem molhadas, e não apenas de canetas de gel, mas também de canetas esferográficas! Economize no papel. Para liberação controle funciona Eu recomendo usar os cadernos do Arkhangelsk Pulp and Paper Mill (18 folhas, gaiola) ou Pyaterochka, embora seja mais caro. É aconselhável escolher uma caneta de gel, mesmo a recarga de gel chinesa mais barata é muito melhor do que uma caneta esferográfica, que mancha ou rasga o papel. A única caneta esferográfica "competitiva" na minha memória é a Erich Krause. Ela escreve com clareza, beleza e estabilidade - seja com uma haste cheia ou com uma quase vazia.

Adicionalmente: a visão de um sistema de coordenadas retangulares através dos olhos da geometria analítica é abordada no artigo (não) dependência linear de vetores. Base vetorial, informações detalhadas sobre quartos de coordenadas podem ser encontradas no segundo parágrafo da lição Desigualdades lineares.

caso 3D

Aqui é quase igual.

1) Desenhamos eixos coordenados. Padrão: aplicar eixo - direcionado para cima, eixo - direcionado para a direita, eixo - para baixo para a esquerda estritamente em um ângulo de 45 graus.

2) Assinamos os eixos.

3) Defina a escala ao longo dos eixos. Escala ao longo do eixo - duas vezes menor que a escala ao longo dos outros eixos. Observe também que no desenho certo, usei uma "serif" não padrão ao longo do eixo (esta possibilidade já foi mencionada acima). Do meu ponto de vista, é mais preciso, rápido e esteticamente mais agradável - você não precisa procurar o meio da célula sob um microscópio e “esculpir” a unidade até a origem.

Ao fazer um desenho 3D novamente - dê prioridade à escala
1 unidade = 2 células (desenho à esquerda).

Para que servem todas essas regras? As regras existem para serem quebradas. O que eu vou fazer agora. O fato é que os desenhos subsequentes do artigo serão feitos por mim no Excel, e os eixos de coordenadas parecerão incorretos em termos de design adequado. Eu poderia desenhar todos os gráficos à mão, mas é realmente assustador desenhá-los, pois o Excel reluta em desenhá-los com muito mais precisão.

Gráficos e propriedades básicas de funções elementares

A função linear é dada pela equação . O gráfico da função linear é direto. Para construir uma reta, basta conhecer dois pontos.

Exemplo 1

Plote a função. Vamos encontrar dois pontos. É vantajoso escolher zero como um dos pontos.

Se então

Tomamos outro ponto, por exemplo, 1.

Se então

Ao preparar tarefas, as coordenadas dos pontos geralmente são resumidas em uma tabela:

E os próprios valores são calculados oralmente ou em um rascunho, calculadora.

Dois pontos são encontrados, vamos desenhar:

Ao elaborar um desenho, sempre assinamos os gráficos.

Não será supérfluo recordar casos especiais de uma função linear:

Observe como coloquei as legendas, assinaturas não devem ser ambíguas ao estudar o desenho. Nesse caso, era altamente indesejável colocar uma assinatura próximo ao ponto de interseção das linhas, ou no canto inferior direito entre os gráficos.

1) Uma função linear da forma () é chamada de proporcionalidade direta. Por exemplo, . O gráfico de proporcionalidade direta sempre passa pela origem. Assim, a construção de uma linha reta é simplificada - basta encontrar apenas um ponto.

2) Uma equação da forma define uma linha reta paralela ao eixo, em particular, o próprio eixo é dado pela equação. O gráfico da função é construído imediatamente, sem encontrar nenhum ponto. Ou seja, a entrada deve ser entendida da seguinte forma: "y é sempre igual a -4, para qualquer valor de x."

3) Uma equação da forma define uma linha reta paralela ao eixo, em particular, o próprio eixo é dado pela equação. O gráfico da função também é construído imediatamente. A entrada deve ser entendida da seguinte forma: "x é sempre, para qualquer valor de y, igual a 1."

Alguns vão perguntar, bem, por que lembrar do 6º ano?! É assim, talvez seja, apenas durante os anos de prática conheci uma boa dúzia de alunos que ficaram perplexos com a tarefa de construir um gráfico como ou .

Desenhar uma linha reta é a ação mais comum ao fazer desenhos.

A linha reta é discutida em detalhes no curso de geometria analítica, e aqueles que desejarem podem consultar o artigo Equação de uma linha reta em um plano.

Gráfico de função quadrática, gráfico de função cúbica, gráfico polinomial

Parábola. Cronograma função quadrática () é uma parábola. Considere o famoso caso:

Vamos relembrar algumas propriedades da função.

Assim, a solução da nossa equação: - é neste ponto que se encontra o vértice da parábola. Por que isso acontece pode ser aprendido com o artigo teórico sobre a derivada e a lição sobre os extremos da função. Enquanto isso, calculamos o valor correspondente de "y":

Então o vértice está no ponto

Agora encontramos outros pontos, usando descaradamente a simetria da parábola. Vale lembrar que a função – não é mesmo, mas, no entanto, ninguém cancelou a simetria da parábola.

Em que ordem encontrar os pontos restantes, acho que ficará claro na mesa final:

Este algoritmo de construção pode ser chamado figurativamente de "shuttle" ou o princípio "de frente e para trás" com Anfisa Chekhova.

Vamos fazer um desenho:

Dos gráficos considerados, outro recurso útil vem à mente:

Para uma função quadrática () o seguinte é verdadeiro:

Se , então os ramos da parábola são direcionados para cima.

Se , então os ramos da parábola são direcionados para baixo.

O conhecimento aprofundado da curva pode ser obtido na lição Hipérbole e parábola.

A parábola cúbica é dada pela função . Aqui está um desenho familiar da escola:

Listamos as principais propriedades da função

Gráfico de funções

Representa um dos ramos da parábola. Vamos fazer um desenho:

As principais propriedades da função:

Neste caso, o eixo é assíntota vertical para o gráfico da hipérbole em .

Será um GRANDE erro se, ao fazer um desenho, por negligência, você permitir que o gráfico se cruze com a assíntota.

Também limites unilaterais, diga-nos que uma hipérbole não limitado de cima e não limitado a partir de baixo.

Vamos explorar a função no infinito: , ou seja, se começarmos a nos mover ao longo do eixo para a esquerda (ou direita) para o infinito, então os “jogos” serão um passo estreito infinitamente perto se aproximam de zero e, consequentemente, os ramos da hipérbole infinitamente perto aproximar do eixo.

Então o eixo é assíntota horizontal para o gráfico da função, se "x" tende a mais ou menos infinito.

A função é ímpar, o que significa que a hipérbole é simétrica em relação à origem. Este fatoé óbvio a partir do desenho, além disso, pode ser facilmente verificado analiticamente: .

O gráfico de uma função da forma () representa dois ramos de uma hipérbole.

Se , então a hipérbole está localizada no primeiro e terceiro quadrantes de coordenadas(veja a imagem acima).

Se , então a hipérbole está localizada no segundo e quarto quadrantes de coordenadas.

Não é difícil analisar a regularidade especificada do local de residência da hipérbole do ponto de vista das transformações geométricas dos gráficos.

Exemplo 3

Construir o ramo direito da hipérbole

Usamos o método de construção pontual, embora seja vantajoso selecionar os valores para que eles se dividam completamente:

Vamos fazer um desenho:

Não será difícil construir o ramo esquerdo da hipérbole, aqui a estranheza da função só ajudará. Grosso modo, na tabela de construção pontual, adicione mentalmente um menos a cada número, coloque os pontos correspondentes e desenhe o segundo ramo.

Informações geométricas detalhadas sobre a linha considerada podem ser encontradas no artigo Hyperbola and parabola.

Gráfico de uma função exponencial

Neste parágrafo, considerarei imediatamente a função exponencial, pois em problemas de matemática superior em 95% dos casos é o expoente que ocorre.

Relembro que - este é um número irracional: , isso será necessário ao construir um gráfico, que, de fato, construirei sem cerimônia. Três pontos provavelmente são suficientes:

Vamos deixar o gráfico da função em paz por enquanto, sobre isso mais tarde.

As principais propriedades da função:

Fundamentalmente, os gráficos das funções parecem os mesmos, etc.

Devo dizer que o segundo caso é menos comum na prática, mas ocorre, então achei necessário incluí-lo neste artigo.

Gráfico de uma função logarítmica

Considere uma função com logaritmo natural.
Vamos fazer um desenho de linha:

Se você esqueceu o que é um logaritmo, consulte os livros escolares.

As principais propriedades da função:

Domínio:

Faixa de valores: .

A função não é limitada a partir de cima: , embora lentamente, mas o ramo do logaritmo vai até o infinito.
Vamos examinar o comportamento da função perto de zero à direita: . Então o eixo é assíntota vertical para o gráfico da função com "x" tendendo a zero à direita.

Certifique-se de conhecer e lembrar o valor típico do logaritmo: .

Fundamentalmente, o gráfico do logaritmo na base parece o mesmo: , , (logaritmo decimal na base 10), etc. Ao mesmo tempo, quanto maior a base, mais plano será o gráfico.

Não vamos considerar o caso, não me lembro quando última vez construiu um gráfico com essa base. Sim, e o logaritmo parece ser um convidado muito raro em problemas de matemática superior.

Para concluir o parágrafo, direi mais um fato: Função Exponencial e Função Logarítmicasão duas funções mutuamente inversas. Se você observar atentamente o gráfico do logaritmo, poderá ver que este é o mesmo expoente, apenas localizado de forma um pouco diferente.

Gráficos de funções trigonométricas

Como o tormento trigonométrico começa na escola? Corretamente. Do seno

Vamos plotar a função

Essa linha é chamada sinusóide.

Relembro que “pi” é um número irracional: e em trigonometria deslumbra aos olhos.

As principais propriedades da função:

Esta funçãoé um periódico com um período. O que isso significa? Vejamos o corte. À esquerda e à direita, exatamente a mesma parte do gráfico se repete infinitamente.

Domínio: , ou seja, para qualquer valor de "x" existe um valor de seno.

Faixa de valores: . A função é limitado: , ou seja, todos os “jogos” ficam estritamente no segmento .
Isso não acontece: ou, mais precisamente, acontece, mas essas equações não têm solução.

Para entender este tópico, considere a função mostrada no gráfico // Vamos mostrar como o gráfico da função permite determinar suas propriedades.

Analisamos as propriedades de uma função usando um exemplo

O escopo da função é yavl. intervalo [ 3,5; 5.5].

O intervalo da função yavl. intervalo [ 1; 3].

1. Em x = -3, x = - 1, x = 1,5, x = 4,5, o valor da função é zero.

O valor do argumento, no qual o valor da função é zero, é chamado de zero da função.

//Essa. para esta função os números -3;-1;1.5; 4,5 são zeros.

2. Nos intervalos [ 4.5; 3) e (1; 1,5) e (4,5; 5,5] o gráfico da função f está localizado acima do eixo de abcissas, e nos intervalos (-3; -1) e (1,5; 4,5) abaixo do eixo de abcissas, isto é explicado da seguinte forma - nos intervalos [ 4.5; 3) e (1; 1.5) e (4.5; 5.5] a função leva valores positivos, e nos intervalos (-3; -1) e (1,5; 4,5) eles são negativos.

Cada um dos intervalos indicados (onde a função assume valores de mesmo sinal) é chamado de intervalo de sinal constante da função f.//i.e. por exemplo, se tomarmos o intervalo (0; 3), então não é um intervalo de sinal constante da função dada.

Em matemática, ao procurar intervalos de sinal constante de uma função, costuma-se indicar intervalos de comprimento máximo. //Aqueles. intervalo (2; 3) é intervalo de constância função f, mas a resposta deve incluir o intervalo [ 4,5; 3) contendo o intervalo (2; 3).

3. Se você se mover ao longo do eixo x de 4,5 a 2, notará que o gráfico da função diminui, ou seja, os valores da função diminuem. //Em matemática, costuma-se dizer que no intervalo [ 4,5; 2] a função está diminuindo.

À medida que x aumenta de 2 para 0, o gráfico da função sobe, ou seja, os valores da função aumentam. //Em matemática, costuma-se dizer que no intervalo [ 2; 0] a função é crescente.

A função f é chamada se para quaisquer dois valores do argumento x1 e x2 deste intervalo tal que x2 > x1, a desigualdade f (x2) > f (x1) é satisfeita. // ou A função é chamada aumentando em algum intervalo, se para quaisquer valores do argumento deste intervalo, o maior valor do argumento corresponde ao maior valor da função.//i.e. quanto mais x, mais y.

A função f é chamada diminuindo em algum intervalo, se para quaisquer dois valores do argumento x1 e x2 deste intervalo tal que x2 > x1, a desigualdade f(x2) decrescente em algum intervalo é satisfeita, se para quaisquer valores do argumento deste intervalo o maior valor do argumento corresponde ao menor valor da função. //Essa. quanto mais x, menos y.

Se uma função é crescente em todo o domínio de definição, então ela é chamada aumentando.

Se uma função é decrescente em todo o domínio de definição, então ela é chamada minguante.

Exemplo 1 gráfico de funções crescentes e decrescentes, respectivamente.

Exemplo 2

Defina yavl. se Função linear f(x) = 3x + 5 crescente ou decrescente?

Prova. Vamos usar as definições. Sejam x1 e x2 valores arbitrários do argumento, e x1< x2., например х1=1, х2=7

Sua privacidade é importante para nós. Por esse motivo, desenvolvemos uma Política de Privacidade que descreve como usamos e armazenamos suas informações. Por favor, leia nossa política de privacidade e deixe-nos saber se você tiver alguma dúvida.

Coleta e uso de informações pessoais

Informações pessoais referem-se a dados que podem ser usados ​​para identificar ou contatar uma pessoa específica.

Você pode ser solicitado a fornecer suas informações pessoais a qualquer momento quando entrar em contato conosco.

A seguir estão alguns exemplos dos tipos de informações pessoais que podemos coletar e como podemos usar essas informações.

Quais informações pessoais coletamos:

• Quando você envia uma inscrição no site, podemos coletar várias informações, incluindo seu nome, número de telefone, endereço E-mail etc.

Como usamos suas informações pessoais:

• As informações pessoais que coletamos nos permitem entrar em contato com você e informá-lo sobre ofertas únicas, promoções e outros eventos e eventos futuros.
• De tempos em tempos, podemos usar suas informações pessoais para enviar avisos e mensagens importantes.
• Também podemos usar informações pessoais para fins internos, como realizar auditorias, análise de dados e várias pesquisas para melhorar os serviços que prestamos e fornecer recomendações sobre nossos serviços.
• Se você participar de um sorteio, concurso ou incentivo semelhante, poderemos usar as informações fornecidas para administrar tais programas.

Divulgação a terceiros

Não divulgamos informações recebidas de você a terceiros.

Exceções:

• Se necessário - de acordo com a lei, ordem judicial, em processos judiciais e/ou com base em solicitações públicas ou solicitações de agências governamentais no território da Federação Russa - divulgue suas informações pessoais. Também podemos divulgar informações sobre você se determinarmos que tal divulgação é necessária ou apropriada para fins de segurança, aplicação da lei ou outros fins de interesse público.
• No caso de uma reorganização, fusão ou venda, podemos transferir as informações pessoais que coletamos para o sucessor terceirizado relevante.

Proteção de informações pessoais

Tomamos precauções - incluindo administrativas, técnicas e físicas - para proteger suas informações pessoais contra perda, roubo e uso indevido, bem como de acesso, divulgação, alteração e destruição não autorizados.

Mantendo sua privacidade no nível da empresa

Para garantir que suas informações pessoais estejam seguras, comunicamos práticas de privacidade e segurança aos nossos funcionários e aplicamos rigorosamente as práticas de privacidade.